General Objective:
Tener conocimiento acerca de los diferentes simuladores de medición .
Specific Objectives:
- Aprender a como usar cada instrumento de medición.
- Obtener por medio de esta simulación conocimientos sobre como usar cada instrumento en la vida real.
- Entender la función de cada instrumento.
Suggested Materials:
- Regla graduada en pulgadas fraccionarias:
- Regla graduada en pulgadas decimales:
- Convertidor de Milímetros a Fracción de Pulgada:
- Paquímetro en milímetros:
- Paquímetro en Fracción de Pulgada:
- Goniómetro de Grado Decimal:
- Goniómetro de Grado No Iónico de un Minuto:
- Micrómetro Milímetro Centesimal:
- Micrómetro de profundidad milímetro centesimal:
- Balanza triple escala:
Approach and procedure:
El grupo de estudiantes practicamos con los distintos simuladores de medida, donde pudimos observar y detallar su función para así obtener conocimiento a la hora de usarlo en la vida real.
Introduction
Los instrumentos de medición son herramientas muy útiles, ya que nos ayudan a calcular magnitudes físicas. Desde la regla común hasta los avanzados dispositivos electrónicos. Estos instrumentos nos permiten obtener datos precisos en áreas como la física, la ingeniería y la ciencia.
Estos permiten la evaluación y comparación de magnitudes físicas como longitud, tiempo, temperatura, presión, electricidad, entre otras. varían en complejidad y principio de funcionamiento. Algunos de los instrumentos más básicos incluyen reglas, cintas métricas y termómetros.
Estos proporcionan mediciones simples y directas, ideales para tareas cotidianas. Sin embargo, en aplicaciones más avanzadas, como la investigación científica o el control de calidad en la industria, se requieren instrumentos más precisos y sofisticados.
Gracias a estos simuladores, pudimos conocer su importancia y el cómo usarlos para así tener un mejor aprendizaje en nuestras distintas áreas donde sean necesarios.
Theoretical framework (books, internet, databases, among others):
Regla graduada en pulgadas fraccionarias: Es una herramienta de medición que se utiliza para medir longitudes en el sistema de unidades imperiales. En lugar de mostrar solo números decimales, como una regla métrica, una regla graduada en pulgadas fraccionarias muestra medidas en pulgadas y fracciones, como 1/4, 1/8, 1/16 de pulgada, permitiendo mediciones más precisas en ese sistema.
Regla graduada en pulgadas decimales: es una herramienta de medición que se utiliza para medir longitudes, pero en lugar de utilizar fracciones, muestra las medidas en pulgadas y decimales. Esto significa que las marcas en la regla representarán incrementos de una pulgada y sub incrementos en décimas o centésimas de pulgada.
Convertidor de milímetros a fracción de pulgada: Este es un dispositivo o herramienta que se utiliza para convertir medidas en milímetros a fracciones de pulgada. Puede ser útil cuando se trabaja con sistemas de unidades diferentes, como el sistema métrico (milímetros) y el sistema imperial (pulgadas).
Paquímetro en milímetros: Un paquímetro es un instrumento de medición utilizado para medir dimensiones lineales con alta precisión. Cuando se utiliza en milímetros, proporciona mediciones precisas en este sistema de unidades.
Paquímetro en fracción de pulgada: Similar al paquímetro en milímetros, pero en lugar de proporcionar mediciones en milímetros, se utiliza para medir en fracciones de pulgada, lo que es común en países que utilizan el sistema imperial de unidades.
Goniómetro de grado decimal: Un goniómetro es un instrumento utilizado para medir ángulos. El goniómetro de grado decimal mide los ángulos en grados, con una precisión de décimas de grado. Es útil en aplicaciones donde se requieren mediciones precisas de ángulos.
Goniómetro de grado no iónico de un minuto: Similar al goniómetro de grado decimal, este tipo de goniómetro mide ángulos, pero con una precisión de un minuto de arco. Un minuto de arco es una unidad de medida angular más pequeña que un grado.
Micrómetro milímetro centesimal: Un micrómetro es un instrumento de medición de alta precisión que se utiliza para medir longitudes extremadamente pequeñas, con una precisión de milésimas de milímetro. Cuando se utiliza en milímetros centesimales, proporciona mediciones precisas en este sistema de unidades.
Micrómetro de profundidad milímetro centesimal: Similar al micrómetro estándar, pero diseñado específicamente para medir la profundidad de agujeros o ranuras con precisión en milímetros centesimales.
Balanza triple escala: Una balanza triple escala es un tipo de balanza que tiene tres escalas de medición diferentes en un solo dispositivo. Esto permite medir el peso de un objeto en tres unidades de medida diferentes, como gramos, onzas y libras, proporcionando versatilidad en la medición de peso.
Description
En base al conocimiento que adquirimos en él aula de clase con cada simulador, la presente práctica de laboratorio tiene como objetivo darnos a conocer distintos instrumentos de medida, cómo aprenderlos a usar y la importancia que tiene en el mundo.
Es fundamental conocer cada instrumento de medición a la perfección y con esta información adquirida se realizó el siguiente trabajo.
Scheme of experiment 1 (draw it)
Regla graduada en pulgadas fraccionarias:
Se ubica el objeto a medir, a lo largo de la regla de observa la marca dónde termina el objeto. A través de eso se interpreta el resultado
Observación:
- En este simulador exploramos una Regla la cual viene graduada en pulgadas (in) y cada pulgada está dividida en 16 partes iguales, lo que implica que cada línea señala 1/16 in.
- Al avanzar una línea hacia la derecha se va aumentando en 1/16 in.
- En la regla se puede apreciar líneas de diferentes tamaños, esas líneas nos ayudan a identificar que numero de dieciseisavo es.
- Sin embargo, al leer las mediciones debemos utilizar su mínima expresión, es decir la fracción más simplificada posible.
- En este caso el ejercicio que muestra la imagen llega a 4 in y su fracción 9/16.
Scheme of experiment 2 (draw it)
Regla graduada en pulgadas decimales:
Se ubica el objeto a medir, a lo largo de la regla de observa la marca dónde termina el objeto. A través de eso se interpreta el resultado.
Observación:
- La escala representada en este simulador está en decimada de pulgada. Esto significa que el numero registrado en la regla representa una pulgada (in) que fue subdividida en décimas.
- En este caso el ejercicio que muestra la imagen es de 1,6 in.
Scheme of experiment 3 (draw it)
Convertidor de Milímetros a Fracción de Pulgada:
Gracias a este simulador lo primero que hicimos fue abrir el convertidor de milímetros a fracción de pulgada, ingresamos la longitud en milímetros que deseamos convertir, presionamos el botón de conversión y el resultado nos mostró la longitud en fracción de pulgada.
Observación:
- En este simulador se arrastra o suelta la línea vertical roja en la horizontal, alineando los valores en las escalas milímetro (mm) o pulgada (in). Luego debajo de ellas, aparecerán los valores en milímetros, fracciones de pulgada y milésimas de pulgada correspondientes y la fórmula para el cálculo.
Scheme of experiment 4 (draw it)
Paquímetro en Milímetros:
Para este simulador aprendimos a abrir el paquímetro y ajústarlo a cero si es necesario, colocar el objeto que deseamos medir entre las mordazas del paquímetro, leer la longitud en milímetros en la escala principal (la escala grande) y si es necesario, verifica la medida en la escala vernier (la escala pequeña), sumar este valor a la medida principal para obtener una mayor precisión.
Observación:
- La escala principal de este simulador esta graduada en centímetros (1 cm) que está dividido por diez milímetros (10 mm). El nonio divide el milímetro por veinte (1/20), marcando cinco centésimas de milímetro (0,005 mm).
Scheme of experiment 5 (draw it)
Paquímetro en Fracción de Pulgada:
Abrir el paquímetro y ajústarlo a cero si es necesario, colocar el objeto que deseas medir entre las mordazas del paquímetro, leer la longitud en fracción de pulgada en la escala principal (la escala grande), si es necesario, verifica la medida en la escala vernier (la escala pequeña) y sumar este valor a la medida principal para obtener una mayor precisión.
Observación:
- La escala principal de este simulador esta graduada en pulgadas (sistema inglés o imperial de medidas británico), que está dividida en fracciones.
- El nonio divide 1/16 in (un dieciseisavo de pulgada) por ocho, marcando la 1/128 in (un ciento y veintiocho de pulgada).
Scheme of experiment 6 (draw it)
Goniómetro de Grado Decimal:
Colocar el goniómetro sobre el objeto o superficie que deseas medir, Alinear el punto cero (0°) con la línea de referencia en el objeto y leer la medida en grados en la escala del goniómetro.
Observación:
- En este simulador, el arco diametral de la llamada escala graduada se divide en 180 espacios equidistantes, llamados’ grado ‘, que son las 180 divisiones de 1° (un grado) grabadas en el cuerpo del instrumento.
Scheme of experiment 7 (draw it)
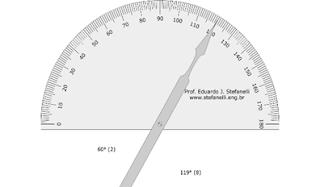
Goniómetro de Grado No Iónico de un Minuto:
Colocar el goniómetro sobre el objeto o superficie que deseas medir, alinea el punto cero (0°) con la línea de referencia en el objeto y leer la medida en grados y minutos en la escala del goniómetro.
Observación:
- En este simulador el diámetro del llamado disco graduado se divide en 360 espacios equidistantes llamados grados, que son los 360 sectores de circunferencias de 1° cada uno.
- Al girar el disco se verá el ángulo formado con una línea fija. En la parte superior del disco hay un nonio o vernier. La marca «cero» (0) de Vernier marca grados enteros de ángulo. El nonio tiene sesenta divisiones relativas a los sesenta minutos (la división de grado) lo que significa que cada trazo ‘marca’ 1 ‘(un minuto).
Scheme of experiment 8 (draw it)
Micrómetro Milímetro Centesimal:
Abre las mordazas del micrómetro y ajústalas a cero si es necesario, colocamos el objeto entre las mordazas del micrómetro, giramos el tambor del micrómetro hasta que las mordazas sujeten firmemente el objeto, lee la medida en milímetros en la escala principal y, si es necesario, en la escala vernier sumar este valor para obtener mayor precisión.
Observación:
- Husillo micrométrico con paso de 0,5 mm y el tambor de 50 divisiones. De este modo, mediante la rotación del husillo micrométrico cada marca del tambor pasa a través de la «línea de referencia» indicará que las puntas de medición se alejan (o aproximan) 0,01 mm (una centésima de milímetro).
Scheme of experiment 9 (draw it)
Micrómetro de profundidad milímetro centesimal:
Abre las mordazas del micrómetro de profundidad y ajústalas a cero si es necesario.
Coloca el extremo del micrómetro sobre la superficie de referencia, gira el tambor del micrómetro hasta que la punta toque la superficie que deseas medir, lee la medida en milímetros en la escala principal y, si es necesario, en la escala vernier sumar el valor para obtener mayor precisión.
Observación:
- El micrómetro no es capaz de tomar las medidas de profundidad sin asociación con otros dispositivos. El mismo husillo milimétrico, y otros componentes, se pueden utilizar para este propósito.
- El aumento en centésimas se realiza en la dirección opuesta a la observada en el micrómetro.
Scheme of experiment 10 (draw it)
Balanza Triple Escala:
Coloca el objeto que deseas pesar en la plataforma de la balanza, ajusta los cursores de las tres escalas (gramos, onzas y newtons) hasta que la balanza esté en equilibrio, lee las lecturas de las tres escalas y registra el peso en las unidades deseadas (gramos, onzas o newtons).
Observación:
- Formada por un único platillo (sujeto de tal forma que sólo pueda desplazarse en vertical) apoyado en un astil dividido en tres partes. Cada una de estas tiene una escala con distinta graduación en este caso gramos (g), a lo largo de la cual se puede desplazar un jinetillo unido a una pesa.
Write your own conclusions (minimum 3):
En el laboratorio de física, la precisión y exactitud en las mediciones son esenciales para obtener resultados confiables y significativos. Durante el desarrollo de este experimento, utilizamos una variedad de herramientas de medición, como la regla graduada en pulgadas fraccionarias, la regla graduada en pulgadas decimales, el convertidor de milímetros a fracción de pulgada, el paquímetro en milímetros, el goniómetro en grados decimales, el micrómetro en centésimas de milímetro y la balanza de triple escala en décimas de gramo. A través de la experiencia práctica, hemos obtenido varias conclusiones importantes:
1. Se logró apreciar que el sistema métrico, representado por el paquímetro en milímetros, ofrece una mayor precisión y resolución en comparación con las herramientas basadas en pulgadas. La capacidad de medir en milímetros permitió registrar longitudes con mayor detalle y exactitud, lo que es especialmente relevante en experimentos que requieren mediciones precisas.
2. Se concluyó El convertidor de milímetros a fracción de pulgada permitió una mayor precisión al representar longitudes en fracciones más detalladas, mejorando así la exactitud en las mediciones.
3. Es importante tener en cuenta la elección de la herramienta correcta depende de la precisión requerida y del tipo de medición a realizar, en este caso las herramientas con una mayor resolución, como el paquímetro y el micrómetro, permiten mediciones más precisas en comparación con las reglas graduadas. La resolución de una herramienta se refiere a la mínima división que puede ser medida. En este sentido, el micrómetro con una resolución de 0,05 mm demostró ser especialmente útil para mediciones altamente precisas.
4. Para medir ángulos con precisión, el goniómetro resultó ser una herramienta confiable. Su uso en grados decimales simplificó la interpretación y el cálculo de mediciones angulares en comparación con sistemas más complejos.
5. Esta práctica resalta la importancia de las herramientas de medición en el laboratorio de física y cómo su correcta utilización puede impactar en la precisión y exactitud de los resultados obtenidos. La elección entre sistemas de unidades, así como la selección de la herramienta más apropiada, deben ser consideradas cuidadosamente para asegurar mediciones confiables y resultados coherentes en futuros experimentos y análisis científicos.
Bibliography:
- Tibanta, M. (2018). Cómo Convertir Milímetros a Fracciones de Pulgada Conocidas. Metal Mecanica Facil.
- Bocanegra, E. (2021). Paquimetros. Dietfarma
- Stefanelli, E. (2019). Nonio o Vernier en fracciones de pulgada uso y lectura. Stefanelli.
- Garza, N. (2022). Qué es un goniómetro y cómo se utiliza. Sdindustrial.
- Zarabozo, V. (2021). ¿Que es un micrometro y como se mide?. Formacion Mecanizdo
- Arroyo, S. (2021). Balanza de triple brazo y volume. Studocu